Eksponen adalah bilangan berpangkat. Contohnya :
#Persamaan Eksponen
Dibawah adalah rumus persamaan eksponen, wajib dihafal ya :
1. b f(x) = b g(x) , maka persamaan akan menjadi : f(x) = g(x)
2. a f(x) = bf(x) , maka persamaan akan menjadi : f(x) = 0
Algoritma
Pada penulisan logaritma alog b = c, a disebut bilangan pokok dan b disebut bilangan numerus atau bilangan yang dicari nilai logaritmanya (b > 0) dan c merupakan hasil logaritma. Jika nilai a sama dengan 10, biasanya 10 tidak dituliskan sehingga menjadi log b = c. Jika nilai bilangan pokoknya merupakan bilangan e (bilangan eurel) dengan e = 2,718281828 maka logaritmanya ditulis dengan logaritma natural dan penulisannya dapat disingkat menjadi ln, misalnya elog b = c menjadi:ln b = c
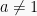 , p > 0, q > 0.
, p > 0, q > 0.
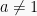 , b > 0
, b > 0

dengan syarat a > 0, 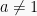 .
.
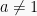 .
.
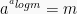 dengan syarat a > 0,
dengan syarat a > 0, 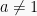 , m > 0.
, m > 0.
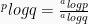 dengan syarat a > 0,
dengan syarat a > 0, 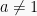 , p > 0, q > 0
, p > 0, q > 0
Nilai Mutlak
Nilai Mutlak yaitu nilai suatu bilangan riil tanpa tanda plus atau minus. Sebagai contoh, nilai absolut dari 3 adalah 3, dan nilai absolut dari –3 juga 3.Misalnya Nilai absolut dari 5 yaitu adalah 5 (jarak dari 0 yaitu 5 unit), Nilai mutlak dari -5 adalah 5 (jarak dari 0: 5 unit).
Simbol untuk nilai mutlak yaitu dua garis lurus, sekitarnya jumlah atau ekspresi yang mengindikasikan nilai mutlak.
Coba pikirkan | x | = 2. Untuk menampilkan x pada garis bilangan, Anda juga harus menunjukkan setiap nomor yang nilainya mutlak adalah 2.
SOAL:
1 . 63 + 62 = ...
63 + 62 = 6(3+2)
= 65 ,maka hasil nya : 7776
2. Hasil dari :
, maka akan di dapat hasilnya : 82 = 64
P itu adalah bilangannya.
n adalah pangkatnya.
Eksponen mempunyai 8 sifat, yaitu :
#Persamaan Eksponen
Dibawah adalah rumus persamaan eksponen, wajib dihafal ya :
1. b f(x) = b g(x) , maka persamaan akan menjadi : f(x) = g(x)
2. a f(x) = bf(x) , maka persamaan akan menjadi : f(x) = 0
3. a f(x) = bg(x) , maka akan menjadi : log a f(x) = log b g(x)
contoh soal:
2.Akar
Pada penulisan logaritma alog b = c, a disebut bilangan pokok dan b disebut bilangan numerus atau bilangan yang dicari nilai logaritmanya (b > 0) dan c merupakan hasil logaritma. Jika nilai a sama dengan 10, biasanya 10 tidak dituliskan sehingga menjadi log b = c. Jika nilai bilangan pokoknya merupakan bilangan e (bilangan eurel) dengan e = 2,718281828 maka logaritmanya ditulis dengan logaritma natural dan penulisannya dapat disingkat menjadi ln, misalnya elog b = c menjadi:ln b = c
contoh:
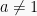 , p > 0, q > 0.
, p > 0, q > 0.
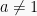 .
.
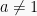 , p > 0, q > 0.
, p > 0, q > 0.
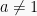 .
.
Sifat-sifat Logaritma
1. Sifat Logaritma dari perkalian
Suatu logaritma merupakan hasil penjumlahan dari dua logaritma lain yang nilai kedua numerus-nya merupakan faktor dari nilai numerus awal. Berikut modelnya:
alog p.q = alog p + alog q
dengan syarat a > 0, 2. Perkalian Logaritma
Suatu logaritma a dapat dikalikan dengan logaritma b jika nilai numerus logaritma a sama dengan nilai bilangan pokok logaritma b. Hasil perkalian tersebut merupakan logaritma baru dengan nilai bilangan pokok sama dengan logaritma a, dan nilai numerus sama dengan logaritma b. Berikut model sifat logaritma nya:
alog b x blog c = alog c
dengan syarat a > 0, 3. Sifat Logaritma dari pembagian
Suatu logaritma merupakan hasil pengurangan dari dua logaritma lain yang nilai kedua numerus-nya merupakan pecahan atau pembagian dari nilai numerus logaritma awal. Berikut modelnya:
alog  = alog p – alog q
= alog p – alog q
dengan syarat a > 0, 4. Sifat Logaritma berbanding terbalik
Suatu logaritma berbanding terbalik dengan logaritma lain yang memiliki nilai bilangan pokok dan numerus-nya saling bertukaran. Berikut modelnya:
alog b = 
dengan syarat a > 0, 5. Logaritma berlawanan tanda
Suatu logaritma berlawanan tanda dengan logaritma yang memiliki numerus-nya merupakan pecahan terbalik dari nilai numerus logaritma awal. Berikut modelnya:
alog  = – alog
= – alog 
dengan syarat a > 0, 6. Sifat Logaritma dari perpangkatan
Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pengali. Berikut modelnya :
alog bp = p. alog b
dengan syarat a > 0, 7. Perpangkatan Bilangan Pokok Logaritma
Suatu logaritma dengan nilai bilangan pokoknya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pembagi. Berikut modelnya:8. Bilangan pokok logaritma sebanding dengan perpangkatan numerus
Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dari nilai bilangan pokoknya memiliki hasil yang sama dengan nilai pangkat numerus tersebut. Berikut model sifat logaritma nya:
alog ap = p
dengan syarat a > 0 dan 9. Perpangkatan logaritma
Suatu bilangan yang memiliki pangkat berbentuk logaritma, hasil pangkatnya adalah nilai numerus dari logaritma tersebut. Berikut modelnya:10. Mengubah basis logaritma
Suatu logaritma dapat dipecah menjadi perbandingan dua logaritma sebagai berikut:Nilai Mutlak
Nilai Mutlak yaitu nilai suatu bilangan riil tanpa tanda plus atau minus. Sebagai contoh, nilai absolut dari 3 adalah 3, dan nilai absolut dari –3 juga 3.Misalnya Nilai absolut dari 5 yaitu adalah 5 (jarak dari 0 yaitu 5 unit), Nilai mutlak dari -5 adalah 5 (jarak dari 0: 5 unit).
Simbol untuk nilai mutlak yaitu dua garis lurus, sekitarnya jumlah atau ekspresi yang mengindikasikan nilai mutlak.
- | 6 | = 6 berarti nilai absolut dari 6 yaitu adalah 6.
- | -6 | = 6 berarti nilai absolut dari negative 6 yaitu adalah 6.
- | -2 – x | berarti nilai absolut dari negative 2 dikurangi x.
- – | x | berarti nilai negatif dari nilai absolut dari x.
Coba pikirkan | x | = 2. Untuk menampilkan x pada garis bilangan, Anda juga harus menunjukkan setiap nomor yang nilainya mutlak adalah 2.
SOAL:
1 . 63 + 62 = ...
63 + 62 = 6(3+2)
= 65 ,maka hasil nya : 7776
2. Hasil dari :
, maka akan di dapat hasilnya : 82 = 64
3.

5(5-4) = 5
4.
Hasil dari adalah ….
adalah ….
![Rendered by QuickLaTeX.com \[ \sqrt{48} + 2 \sqrt{27} - \sqrt{147} = \sqrt{16 \times 3} + 2 \sqrt{9 \times 3} - \sqrt{49 \times 3} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2a9a2ded450b084fead2bdafa08736bf_l3.svg)
5.Bentuk dirasionalkan penyebutnya mempunyai hasil ….
dirasionalkan penyebutnya mempunyai hasil ….
![Rendered by QuickLaTeX.com \[ \frac{2}{\sqrt{6}} = \frac{2}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-dead2b3883a2009b9fb2fc8182b5fa2d_l3.svg)
![Rendered by QuickLaTeX.com \[ = \frac{2 \sqrt{6}}{6} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-6706b4396f21cb4326e64d6ef0f18d57_l3.svg)
![Rendered by QuickLaTeX.com \[ = \frac{1 \sqrt{6}}{3} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-5c129305419a3357027b3a2a75612154_l3.svg)
![Rendered by QuickLaTeX.com \[ = \frac{1}{3} \sqrt{6} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-1ec8e0d4c56210c4b93e7a21f8664e61_l3.svg)
6.Hasil dari adalah ….
adalah ….
![Rendered by QuickLaTeX.com \[ \sqrt{300} : \sqrt{6} = \sqrt{\frac{300}{6}} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-97e13ae9d30face570ec4aca886e7dd3_l3.svg)
![Rendered by QuickLaTeX.com \[ = \sqrt{50} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-64d8486601ce82ca59af9640108c3b17_l3.svg)
![Rendered by QuickLaTeX.com \[ = \sqrt{25 \times 2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-f6370fbbc534b6839a689d870f166786_l3.svg)
![Rendered by QuickLaTeX.com \[ = \sqrt{25}\sqrt{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-5cae5b988029056b56aea602dd80eee3_l3.svg)
![Rendered by QuickLaTeX.com \[ = 5\sqrt{2} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2352a1a7a78b1fefe532126d8269ef86_l3.svg)
7.1. Diketahui log 3 = 0,332 dan log 2 = 0,225.maka log 18 dari soal tersebut adalah……..
Diket :
Log 3 = 0,332
Log 2 = 0,225
Ditanya: log 18 =…………….?
Jawaban:
Log 18 = log 9 . log 2
Log 18 = (log 3.log 3) . log 2
Log 18 = 2 . (0,332) + (0,225)
Log 18 = 0,664 + 0,225
Log 18 = 0,889
8. Ubahlah bentuk pangkat pada soal-soal berikut ini ke dalam bentuk logaritma:
Pembahasannya :
Jika nilai ba = c, maka nilai untuk blog c = a
Jawaban :
|2x – 1| = |x + 4|
2x – 1 = x + 4 ataupun 2x – 1 = -(x + 4)
x = 5 ataupun 3x = -3
x = 5 ataupun x = -1
Maka, HP = (-1, 5)
10. Tentukanlah himpunan penyelesaian |2x – 7| = 3
Jawaban :
|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)
|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)
|2x – 7| = 3 ( x = 5 ataupun x = 2)
Maka, HP = 2, 5

5(5-4) = 5
4.
Hasil dari
5.Bentuk
6.Hasil dari
7.1. Diketahui log 3 = 0,332 dan log 2 = 0,225.maka log 18 dari soal tersebut adalah……..
Diket :
Log 3 = 0,332
Log 2 = 0,225
Ditanya: log 18 =…………….?
Jawaban:
Log 18 = log 9 . log 2
Log 18 = (log 3.log 3) . log 2
Log 18 = 2 . (0,332) + (0,225)
Log 18 = 0,664 + 0,225
Log 18 = 0,889
8. Ubahlah bentuk pangkat pada soal-soal berikut ini ke dalam bentuk logaritma:
Pembahasannya :
Jika nilai ba = c, maka nilai untuk blog c = a
- 24 = 16 → 2log 16 = 4
- 58 = 675 → 5log 675 = 8
- 27 = 48 → 2log 48 = 7
Jawaban :
|2x – 1| = |x + 4|
2x – 1 = x + 4 ataupun 2x – 1 = -(x + 4)
x = 5 ataupun 3x = -3
x = 5 ataupun x = -1
Maka, HP = (-1, 5)
10. Tentukanlah himpunan penyelesaian |2x – 7| = 3
Jawaban :
|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)
|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)
|2x – 7| = 3 ( x = 5 ataupun x = 2)
Maka, HP = 2, 5












Komentar
Posting Komentar